In the early years of violin playing, F natural = F sharp and B flat = B natural - always. Never mind all these imagined enharmonic subtleties. 






 = F
= F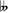 , for instance; in these tunings it is not true that E♯ = F♮, which is characteristic only of 12 equal temperament.[original research?]
, for instance; in these tunings it is not true that E♯ = F♮, which is characteristic only of 12 equal temperament.[original research?]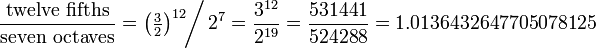
 . Then high C has a frequency of
. Then high C has a frequency of  . The 1/4 comma meantone has just (i.e., perfectly tuned) major thirds, which means major thirds with a frequency ratio of exactly 4 to 5.
. The 1/4 comma meantone has just (i.e., perfectly tuned) major thirds, which means major thirds with a frequency ratio of exactly 4 to 5.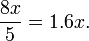

 .
.  . Such small differences in pitch can escape notice when presented as melodic intervals. However, when they are sounded as chords, the difference between meantone intonation and equal-tempered intonation can be quite noticeable, even to untrained ears.
. Such small differences in pitch can escape notice when presented as melodic intervals. However, when they are sounded as chords, the difference between meantone intonation and equal-tempered intonation can be quite noticeable, even to untrained ears.
Comment